Create a kNN Model

Command:

Math -> Memory Based Learner (kNN) -> Create Model

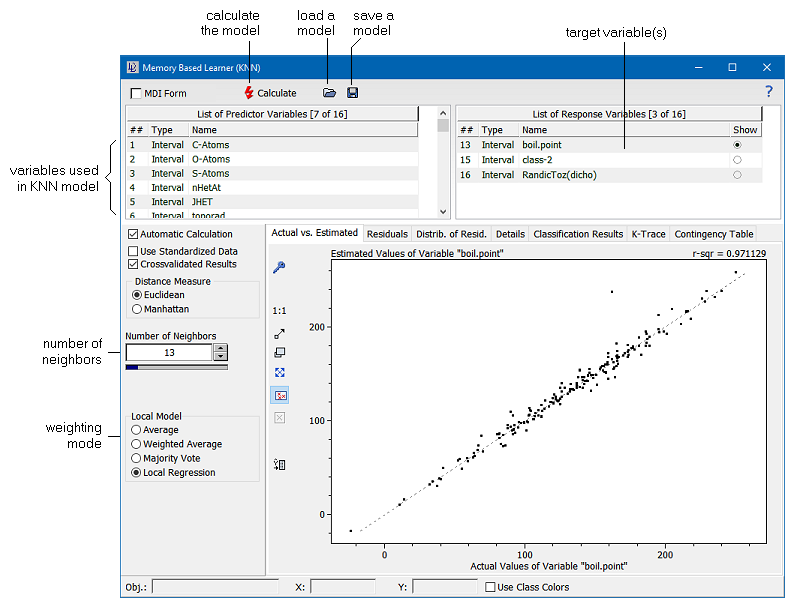
The command Math/Memory Based Learner (kNN) provides the capability of building models based on the well-known kNN paradigma and applying them to unknown data. The user has the choice of several methods for estimating the results from the nearest neighbors. Although the kNN method normally is used for classification purposes only, DataLab makes an attempt to exploit the ideas behind kNN also for the estimation of continuous properties.

The basic approach to kNN modelling is first to compile the data which should serve as a model, then to build a model from the data, and finally to apply this model to unknown data by means of the kNN Applicator.

The number of neighbors can be adjusted by the scrollbar between 1 and 100. Please note that for majority voting the number of neighbors should be odd.

The weighting mode determines the procedure for calculating the estimated value from its nearest neighbors. DataLab provides four methods for estimating the unknown values: (1) by calculating the average, (2) by calculating a weighted average, (3) by performing a majority voting amongst the nearest neighbors, and (4) by building a local linear regression model.

Majority voting is normally used for classification purposes only. In this case that class is assigned to the unknown which has a majority among the classes of the k nearest neighbors. This concept can be extended to the continuous approximation case by introducing density distribution estimators of the target values among the set of nearest neighbors. DataLab provides such an estimation of density distributions. Thus majority voting can also be applied to continuous data, though a better way to estimate continuous data from kNN models is to use local regression models.

The local linear regression is a simple method of estimating non-linear functional dependencies by the combination of kNN and multiple linear regression. The idea behind this method is simple: the nearest neighbors found for a given unknown data point are used to set up a linear model by the use of multiple linear regression. This model is then used to predict the target value of the unknown. A natural prerequisite of this method is of course that the number of nearest neighbors determined must exceed the number of input variables of the model. Under practical circumstances we recommend to use at least twice the number of neighbors than the number of descriptors (to avoid overfitting).