Multiples Regressionsmodell
Angenommen Sie möchten ein mathematisches Modell aufstellen, das den Siedepunkt chemischer Substanzen aus einigen Strukturparametern abschätzt. Ein solches Modell hätte den Vorteil, dass man den Siedepunkt einer Substanz schätzen kann, ohne die Substanz physisch zur Verfügung zu haben (selbst wenn es die Substanz noch gar nicht gibt, wäre eine Abschätzung des Siedepunktes möglich).
Dazu benötigen wir zuerst einmal einen Musterdatensatz mit Strukturparametern (die aus der chemischen Struktur errechnet werden können) und die zugehörigen Siedepunkte. Unser Musterdatensatz umfasst 185 Substanzen, von denen jeweils 12 Strukturparameter berechnet worden sind und die Siedepunkte bekannt sind.
Bei der Erstellung des Modells ist eine der zentralen Fragen, welche der 12 Parameter sind am besten zur Erstellung des Modells geeignet. DataLab bietet zur Auswahl der geeigneten Variablen folgende Methoden an: Vorwärtsselektion, Rückwärtselimination, schrittweise Regression und der Test aller möglichen Variablenkombinationen. Wir rufen dazu den Befehl "Mathematik/Multiple Lineare Regression/Variablenauswahl" auf (oder Knopf  in der Schnellstartleiste).
in der Schnellstartleiste).
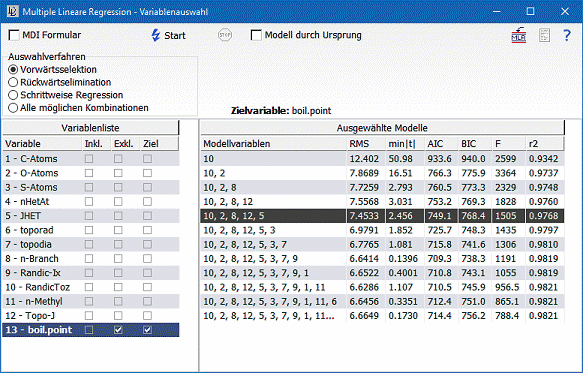
 ) und dort das Modell berechnen:
) und dort das Modell berechnen:
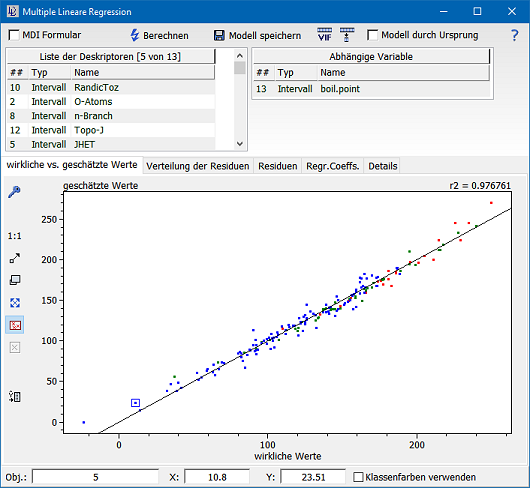
Die Detailergebnisse der multiplen Regression können über das Protokoll (Knopf  ) abgerufen werden:
) abgerufen werden:
============================================================
Multiple Lineare Regression: d:\datalab\data\boilpts.idt
============================================================
Zahl der Objekte ................: 185
Zahl der Eingangsvariablen ......: 5
Zahl der Freiheitsgrade .........: 179
Abhängige Variable ..............: [13] boil.point
Mittelwert der Zielwerte ........: 132.714054
Standardabw. der Zielwerte ......: 48.223876
Mittelwert der gesch. Werte .....: 132.714054
Standardabw. der gesch. Werte ...: 47.660251
Standardabw. der Residuen .......: 7.4533
Bestimmtheitsmaß ................: 0.9768
korrigiertes Bestimmtheitsmaß ...: 0.9762
F-Wert ..........................: 1504.731 (p=0.0000)
Durbin-Watson Testgröße: 1.27485
kritische Werte (alpha=0.05): DL=1.69295 DU=1.82670
*** Die Residuen sind seriell korreliert.
------------------------------------------------------------
ANOVA DF sum of squares mean square F
------------------------------------------------------------
Regression 5 4.17956E+05 8.35912E+04 1504.731
Residual 179 9.94385E+03 5.55522E+01
Total 184 4.27900E+05
------------------------------------------------------------
Regressionskoeffizienten:
Spalte Var.Name Koeffizient +/- Std.Fehler(Koeff) t-Test alpha
------------------------------------------------------------------------
- INTERCEPT -7.0960574E+01 +/- 5.5103328E+00 -12.878 0.0000
10 RandicToz 7.6873275E+00 +/- 1.1242126E-01 68.380 0.0000
2 O-Atoms -1.3123226E+01 +/- 7.9273468E-01 -16.554 0.0000
8 n-Branch -4.6668763E+00 +/- 1.1711391E+00 -3.985 0.0001
12 Topo-J 7.2078089E+00 +/- 2.3775368E+00 3.032 0.0028
5 JHET -8.5553223E-01 +/- 3.4827518E-01 -2.456 0.0150
 Epina DataLab
Epina DataLab